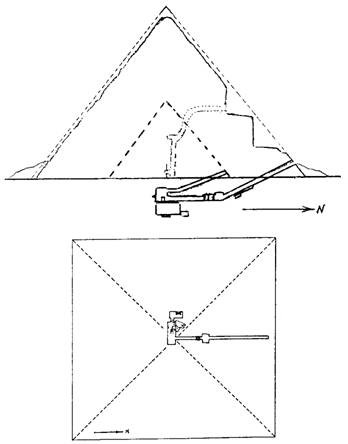
Hauteur de la pyramide Comment le trouver?

Une pyramide est un polyèdre, à la base duquelse trouve le polygone. À leur tour, tous les visages forment des triangles qui convergent vers un sommet. Les pyramides sont triangulaires, quadrangulaires et ainsi de suite. Afin de déterminer quelle pyramide est en face de vous, il suffit de calculer le nombre de coins à sa base. La définition de «hauteur de la pyramide» est très souvent rencontrée dans les problèmes de géométrie du programme scolaire. Dans cet article, nous allons essayer d'envisager différentes façons de le trouver.

Parties de la pyramide

Chaque pyramide est composée des éléments suivants:

• faces latérales qui ont trois coins et convergent au sommet;
• l'apophème est la hauteur qui descend de son apex;
• le sommet de la pyramide est le point qui relie les bords latéraux, mais ne se trouve pas dans le plan de la base;
• la base est un polygone sur lequel le sommet ne ment pas;
• la hauteur de la pyramide est un segment qui traverse le sommet de la pyramide et forme un angle droit avec sa base.

Comment trouver la hauteur d'une pyramide, si son volume est connu

Par la formule de volume de la pyramide V = (S * h) / 3 (enV est le volume, S est la surface de la base, et h est la hauteur de la pyramide), on trouve que h = (3 * V) / S. Pour résoudre le problème, résolvons le problème immédiatement. Dans la pyramide triangulaire, la surface de la base est de 50 cm², alors que son volume est de 125 cm³. La hauteur de la pyramide triangulaire est inconnue, et nous devons le trouver. Ici tout est simple: on colle les données dans notre formule. On obtient h = (3 * 125) / 50 = 7,5 cm.

Comment trouver la hauteur d'une pyramide si la longueur de la diagonale et ses arêtes sont connues

Comme nous le rappelons, la hauteur de la pyramide se forme avecpar l'angle de base. Et cela signifie que la hauteur, le bord et la moitié de la diagonale forment ensemble un triangle rectangulaire. Beaucoup, bien sûr, se souviennent du théorème de Pythagore. Connaissant les deux dimensions, la troisième valeur ne sera pas difficile à trouver. Rappelons le théorème bien connu a² = b² + c², où a est l'hypoténuse, et dans notre cas le bord de la pyramide; b - la première jambe ou la moitié de la diagonale et avec - respectivement, la deuxième jambe, ou la hauteur de la pyramide. De cette formule, c² = a² - b².

Maintenant, le problème: dans la bonne pyramide, la diagonale est de 20 cm, alors que la longueur de la côte - 30 cm.Il est nécessaire de trouver la hauteur. Nous décidons: c² = 30² - 20² = 900-400 = 500. Donc c = √ 500 = environ 22,4.

Comment trouver la hauteur d'une pyramide tronquée

C'est un polygonea une section parallèle à sa base. La hauteur de la pyramide tronquée est un segment qui relie ses deux bases. La hauteur peut être trouvée dans la pyramide correcte si les longueurs des diagonales des deux bases sont connues, ainsi que le bord de la pyramide. Supposons que la diagonale de la plus grande base soit d1, tandis que la diagonale de la plus petite base soit d2 et que le bord ait la longueur-l. Pour trouver la hauteur, il est possible d'abaisser les hauteurs sur sa base à partir des deux points opposés supérieurs du diagramme. Nous voyons que nous avons fait deux triangles rectangulaires, il reste à trouver la longueur de leurs jambes. Pour ce faire, à partir de la plus grande diagonale, soustraire le plus petit et diviser par 2. Nous trouvons donc une coupe: a = (d1-d2) / 2. Après cela, par le théorème de Pythagore, nous avons seulement besoin de trouver la seconde jambe, qui est la hauteur de la pyramide.

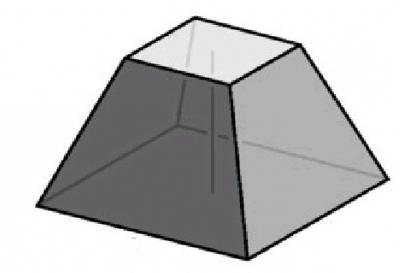
Maintenant, regardons tout cela en pratique. Avant nous est la tâche. La pyramide tronquée a un carré dans la base, la longueur de la diagonale de la plus grande base est de 10 cm, tandis que la plus petite - 6 cm, et le bord est de 4 cm.Il est nécessaire de trouver la hauteur. Premièrement, nous trouvons une cathète: a = (10-6) / 2 = 2 cm, une cathète est de 2 cm et l'hypoténuse de 4 cm, il s'avère que la seconde jambe ou hauteur sera 16-4 = 12, c'est-à-dire h = √12 = environ 3,5 cm.