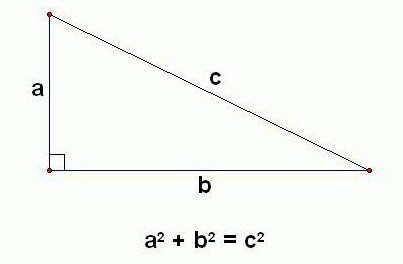
Le théorème du cosinus et sa preuve

Chacun d'entre nous assis pendant de nombreuses heures au cours de la décisiontelle ou telle tâche de géométrie. Bien sûr, la question se pose: pourquoi avez-vous besoin d'apprendre les mathématiques? La question est particulièrement pertinente pour la géométrie, dont la connaissance, si elle est utile, est très rare. Mais les mathématiques ont un rendez-vous pour ceux qui ne vont pas devenir un employé des sciences exactes. Cela fait travailler et développer une personne.

Le but initial des mathématiques n'était pasdonner aux étudiants la connaissance du sujet. Les enseignants se fixent comme objectif d'apprendre aux enfants à penser, raisonner, analyser et discuter. C'est ce que nous trouvons en géométrie avec ses nombreux axiomes et théorèmes, conséquences et preuves.

Le théorème du cosinus

Simultanément aux fonctions trigonométriques etLes inégalités de l'algèbre commencent à étudier les angles, leur signification et leur localisation. Le théorème du cosinus est l'une des premières formules qui lie les deux côtés de la science mathématique dans la compréhension de l'étudiant.

Pour trouver le côté par les deux autres et le coinentre eux, le théorème du cosinus est appliqué. Pour un triangle avec un angle droit, le théorème de Pythagore nous convient également, mais si nous parlons d'un chiffre arbitraire, alors il ne peut pas être appliqué ici.

Le théorème du cosinus est le suivant:

AC ²= AB ²+ Soleil ²- 2 * AB * BC * cos <ABC

Le carré d'un côté est égal à la somme des deux autres côtés pris dans le carré, moins leur produit, multiplié par deux et par le cosinus de l'angle qu'ils forment.

Si vous regardez de plus près, celala formule ressemble au théorème de Pythagore. En effet, si nous prenons l'angle entre les jambes pour être 90, alors la valeur de son cosinus sera 0. En conséquence, seule la somme des carrés des côtés restera, ce qui est reflété par le théorème de Pythagore.

Le théorème du cosinus: Preuve.

De cette expression nous dérivons la formule AC ² et nous obtenons:

AC ² = ВС ² + AB ² - 2 * AB * BC * cos <ABC

Ainsi, on voit que l'expression correspond àla formule ci-dessus, qui indique sa vérité. Nous pouvons dire que le théorème du cosinus est prouvé. Il est utilisé pour toutes sortes de triangles.

Utilisation

En plus des leçons de mathématiques et de physique, cetteLe théorème est largement utilisé dans l'architecture et la construction, pour calculer les côtés et les angles nécessaires. Avec son aide déterminer les dimensions nécessaires du bâtiment et le nombre de matériaux qui seront nécessaires pour son érection. Bien sûr, la plupart des processus qui nécessitaient auparavant une participation humaine directe et des connaissances sont automatisés à ce jour. Il existe un grand nombre de programmes qui vous permettent de simuler des projets similaires sur votre ordinateur. Leur programmation est également effectuée en tenant compte de toutes les lois, propriétés et formules mathématiques.

D

</ p>